Pembahasan Soal SBMPTN tahun 2017 untuk Tes Kemampuan Dasar dan Potensi Akademik (TKPA) kode naskah 226 mata uji Matematika Dasar.
Materi uji meliputi : Matriks, Pertidaksamaan nilai mutlak, Geometri datar (segitiga), Aljabar fungsi (domain), Statistika, Barisan aritmatika, Aplikasi turunan, Barisan/deret geometri, Fungsi komposisi (range), Dimensi tiga, SPLDV, Transformasi geometri, Integral tak tentu, Limit tak tentu, Kaedah pencacahan.
1. SBMPTN 2017 Matriks
Misalkan AT adalah transpos matriks A. Jika \(\mathrm{A=\begin{pmatrix}
2 & \mathrm{{\color{white} -}x}\\
0 & -2
\end{pmatrix}}\) sehingga \(\mathrm{A^{T}A=\begin{pmatrix}
4 & 4\\
4 & 8
\end{pmatrix}}\), maka nilai x2 - x adalah ...
(A) 0
(B) 2
(C) 6
(D) 12
(E) 20
Pembahasan :
\(\mathrm{A^{T}A=\begin{bmatrix}
4 & 4\\
4 & 8
\end{bmatrix}}\)
\(\begin{bmatrix}
2 & \mathrm{{\color{white} -}x}\\
0 & -2
\end{bmatrix}^{T}\begin{bmatrix}
2 & \mathrm{{\color{white} -}x}\\
0 & -2
\end{bmatrix}=\begin{bmatrix}
4 & 4\\
4 & 8
\end{bmatrix}\)
\(\begin{bmatrix}
2 & {\color{white} -}0\\
\mathrm{x} & -2
\end{bmatrix}\begin{bmatrix}
2 & \mathrm{{\color{white} -}x}\\
0 & -2
\end{bmatrix}=\begin{bmatrix}
4 & 4\\
4 & 8
\end{bmatrix}\)
\(\begin{bmatrix}
4 & \mathrm{2x}\\
\mathrm{2x} & \mathrm{x^{2}}+4
\end{bmatrix}=\begin{bmatrix}
4 & 4\\
4 & 8
\end{bmatrix}\)
Dari persamaan matriks diatas diperoleh
2x = 4 → x = 2
Jadi, (x2 - x) = (22 - 2) = 2
Jawaban : B
2. SBMPTN 2017 Pertidaksamaan Nilai mutlak
Jika himpunan penyelesaian \(\mathrm{|2x-\mathit{a}|<5}\) adalah \(\left \{ \mathrm{x/-1<x<4} \right \}\), maka nilai a adalah ...
A. -4 D. 3
B. -3 E. 4
C. -1
Pembahasan :
Untuk k konstan dan k > 0, berlaku :
| f(x) | < k ⟺ -k < f(x) < k
Berdasarkan sifat diatas maka
| 2x - a | < 5 ⟺ -5 < 2x - a < 5
| 2x - a | < 5 ⟺ a - 5 < 2x < a + 5
| 2x - a | < 5 ⟺ \(\frac{a-5}{2}\) < x < \(\frac{a+5}{2}\)
Karena -1 < x < 4 maka haruslah
\(\frac{a-5}{2}\) = -1 atau \(\frac{a+5}{2}\) = 4
Dari persamaan diatas diperoleh a = 3.
Jawaban : D
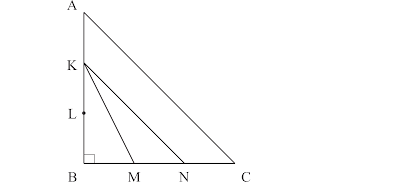
3. SBMPTN 2017 Geometri Datar : Segitiga
Pada segitiga siku-siku samakaki ABC, sisi AB dan BC masing-masing terbagi menjadi tiga bagian yang sama, berturut-turut oleh titik K, L, dan M, N. Jika luas ΔABC adalah x cm2, maka luas ΔKMN adalah ... cm2.
(A) \(\mathrm{\frac{x}{3}}\)
(B) \(\mathrm{\frac{2x}{9}}\)
(C) \(\mathrm{\frac{x}{9}}\)
(D) \(\mathrm{\frac{x}{18}}\)
(E) \(\mathrm{\frac{x}{36}}\)
Pembahasan :
L ΔABC = \(\frac{1}{2}\)(BC)(AB) = x
MN = \(\frac{1}{3}\)BC dan KB = \(\frac{2}{3}\)AB
L ΔKMN = \(\frac{1}{2}\)(MN)(KB)
L ΔKMN = \(\frac{1}{2}\) (\(\frac{1}{3}\)BC) (\(\frac{2}{3}\)AB)
L ΔKMN = \(\frac{2}{9}\) . \(\frac{1}{2}\)(BC)(AB)
L ΔKMN = \(\frac{2}{9}\) . x
L ΔKMN = \(\mathrm{\frac{2x}{9}}\)
Jawaban : B
4. SBMPTN 2017 Aljabar Fungsi : Domain
Jika f(x) = x2 - 1 dan g(x) = \(\mathrm{\frac{x\,-\,2}{x\,+\,1}}\), maka daerah asal fungsi f.g adalah ...
(A) {x/ -∞ < x < ∞}
(B) {x/ x ≠ -1}
(C) {x/ x ≠ 2}
(D) {x/ x < -1}
(E) {x/ x ≥ 2}
Pembahasan :
Misalkan daerah asal (domain) fungsi f adalah Df dan domain fungsi g adalah Dg. Jika domain fungsi f.g dan f/g berturut-turut adalah Df.g dan Df/g, maka :
Df.g = Df ∩ Dg
Df/g = Df ∩ Dg ∩ g ≠ 0
f(x) = x2 - 1 → Df = {x ∈ ℝ}
g(x) = \(\mathrm{\frac{x\,-\,2}{x\,+\,1}}\) → Dg = {x ≠ -1}
Df.g = Df ∩ Dg
Df.g = {x ∈ ℝ} ∩{x ≠ -1}
Df.g = {x ≠ -1}
Jawaban : B
5. SBMPTN 2017 Statistika
Diketahui median dan rata-rata berat badan 5 balita adalah sama. Setelah ditambahkan satu data berat badan balita, rata-ratanya meningkat 1 kg, sedangkan mediannya tetap. Jika 6 data berat badan tersebut diurutkan dari yang paling ringan ke yang paling berat, maka selisih berat badan antara balita terakhir yang ditambahkan dan balita di urutan ke-4 adalah ... kg.
(A) 4
(B) \(\frac{9}{2}\)
(C) 5
(D) 6
(E) \(\frac{13}{2}\)
Pembahasan :
Misalkan berat badan 5 balita setelah diurutkan adalah a, b, c, d, e dan berat badan balita terakhir yang ditambahkan adalah x.
Median dari 5 data a, b, c, d, e adalah c.
Rata-rata berat badan ke-5 balita adalah \(\mathrm{\frac{a+b+c+d+e}{5}}\).
Rata-rata berat badan setelah ditambahkan 1 balita yang beratnya x adalah \(\mathrm{\frac{a+b+c+d+e+x}{6}}\).
Karena median dan rata-rata ke-5 balita sama, maka :
c = \(\mathrm{\frac{a+b+c+d+e}{5}}\) atau a + b + c + d + e = 5c
Karena rata-rata meningkat 1 kg setelah ditambahkan 1 balita, diperoleh persamaan
\(\mathrm{\frac{a+b+c+d+e}{5}}\) + 1 = \(\mathrm{\frac{a+b+c+d+e+x}{6}}\)
c + 1 = \(\mathrm{\frac{5c+x}{6}}\)
6c + 6 = 5c + x
x = c + 6
Karena x = c + 6, maka x > c. Akibatnya, x tidak mungkin menempati urutan 1, 2 atau 3.
Agar median sesudah ditambahkan 1 data nilainya tetap, maka berat badan urutan ke-3, yaitu c harus sama dengan berat badan urutan ke-4, dengan alasan median dari 6 data dihitung dari \(\mathrm{\frac{U_{3}+U_{4}}{2}}\). Akibatnya, x bukan urutan ke-4 karena x ≠ c. Jadi, urutan ke-4 adalah d, dengan d = c.
Dengan demikian, selisih berat badan antara balita terakhir yang ditambahkan dan balita di urutan ke-4 adalah x - d = (c + 6) - (c) = 6.
Jawaban : D
6. SBMPTN 2017 Barisan Aritmatika
Suku ke-11 suatu barisan aritmatika sama dengan empat kali suku ke-16. Jika beda barisan tersebut adalah -3, maka empat kali suku ke-14 sama dengan suku ke...
(A) 1
(B) 3
(C) 5
(D) 7
(E) 9
Pembahasan :
Rumus suku ke-n barisan aritmatika adalah
Un = a + (n - 1)b
a = suku pertama
b = beda
Diketahui suku ke-11 sama dengan empat kali suku ke-16, kita tulis
U11 = 4 U16
a + 10b = 4(a + 15b)
a + 10b = 4(a + 13b + 2b)
a + 10b = 4(U14 + 2b)
a + 10b = 4U14 + 8b
a + 2b = 4U14
U3 = 4U14
Jadi, empat kali suku ke-14 sama dengan suku ke-3
Jawaban : B
7. SBMPTN 2017 Aplikasi Turunan
Seseorang memelihara ikan di suatu kolam. Rata-rata bobot ikan per ekor pada saat panen dari kolam tersebut adalah (6 - 0,02x) kg, dengan x menyatakan banyak ikan yang dipelihara. Maksimum total bobot semua ikan pada saat panen yang mungkin adalah ... (kg)
(A) 400
(B) 420
(C) 435
(D) 450
(E) 465
Pembahasan :
Misalkan total bobot semua ikan adalah Y. Jika x menyatakan banyak ikan yang dipelihara, maka rata-rata bobot ikan per ekor adalah \(\mathrm{\frac{Y}{x}}\). Karena rata-rata bobot ikan per ekor adalah (6 - 0,02x), maka :
\(\mathrm{\frac{Y}{x}}\) = (6 - 0,02x)
Y = (6 - 0,02x)x
Y = 6x - 0,02x2
Total bobot semua ikan akan maksimum jika Y' = 0
6 - 0,04x = 0 (kali 100)
600 - 4x = 0
⇒ x = 150
Jadi, maksimum total bobot semua ikan pada saat panen yang mungkin adalah
Y = 6(150) - 0,02(150)2 = 450 kg.
Jawaban : D
8. SBMPTN 2017 Barisan dan Deret Geometri
Perbandingan suku ke-6 terhadap suku pertama suatu barisan geometri adalah 1/32. Jika jumlah suku ke-3 dan suku ke-4 adalah 15, maka jumlah 3 suku pertama barisan tersebut adalah ...
(A) 30
(B) 40
(C) 50
(D) 60
(E) 70
Pembahasan :
Rumus suku ke-n barisan geometri adalah
Un = arn-1
a = suku pertama
r = rasio
Diketahui \(\mathrm{\frac{U_{6}}{U_{1}}=\frac{1}{32}}\), dapat ditulis
\(\mathrm{\frac{ar^{5}}{a}=\frac{1}{32}}\)
\(\mathrm{r^{5}=\left (\frac{1}{2} \right )^{5}}\)
⇒ r = \(\frac{1}{2}\)
Diketahui U3 + U4 = 15, dapat ditulis
ar2 + ar3 = 15
a(\(\frac{1}{2}\))2 + a(\(\frac{1}{2}\))3 = 15 (kali 8)
2a + a = 120
⇒ a = 40
Diperoleh suku pertama 40 dan rasio \(\frac{1}{2}\), sehingga barisannya adalah
40, 20, 10, ...
Jadi, jumlah 3 suku pertama adalah
40 + 20 + 10 = 70
Jawaban : E
9. SBMPTN 2017 Fungsi Komposisi : Range
Jika f(x) = 1 - x2 dan g(x) = \(\sqrt{5\,-\,\mathrm{x}}\), maka daerah hasil fungsi komposisi fog adalah ...
(A) {y/ -∞ < y < ∞}
(B) {y/ y ≤ -1 atau y ≥ 1}
(C) {y/ y ≤ 5}
(D) {y/ y ≤ 1}
(E) {y/ 1 ≤ y ≤ 1}
Pembahasan :
Untuk menentukan daerah hasil (range) fungsi komposisi fog, dapat kita mulai dengan menentukan domainnya terlebih dahulu.
fog(x) = f(\(\sqrt{5\,-\,\mathrm{x}}\))
fog(x) = 1 - (\(\sqrt{5\,-\,\mathrm{x}}\))2 → Dfog = {5 - x ≥ 0} = {x ≤ 5}
fog(x) = 1 - (5 - x)
fog(x) = x - 4
Catatan : Domain fungsi komposisi diperoleh sebelum fungsi disederhanakan (penyederhanaan yang dimaksud adalah penyederhanaan yang merubah domain fungsi, seperti menghilangkan tanda akar atau mencoret penyebut). Jika ingin menentukan domain setelah fungsi komposisi disederhanakan, maka domain yang diperoleh harus diiris kembali dengan domain fungsi input (untuk kasus diatas fungsi inputnya adalah g(x)).
Diatas telah diperoleh y = fog = x - 4, dengan domain x ≤ 5. Untuk daerah hasilnya, dapat ditentukan dengan memanipulasi domain fog.
x ≤ 5 (kurangkan kedua ruas dengan 4)
x - 4 ≤ 5 - 4
x - 4 ≤ 1
y ≤ 1 (karena y = x - 4)
Jawaban : D
10. SBMPTN 2017 Dimensi Tiga
Diketahui kubus ABCD.EFGH dengan P dan Q berturut-turut adalah titik tengah HG dan BC. Jika panjang rusuk kubus tersebut adalah 4 cm, maka jarak P ke Q adalah ... cm.
(A) 2√3
(B) 2√6
(C) 6√2
(D) 6√3
(E) 6√6
Pembahasan :
Perhatikan gambar !
RQ2 = RC2 + CQ2 = 22 + 22 = 8
Perhatikan segitiga PRQ siku-siku di R.
PQ2 = PR2 + RQ2
PQ2 = 16 + 8
PQ2 = 24
PQ = √(24) = 2√6
Jawaban : B
11. SBMPTN 2017 SPLDV
Luas daerah penyelesaian sistem pertidaksamaan
x + y ≤ 3, 3x + 2y ≥ 6, y ≥ 0 adalah ... satuan luas.
(A) \(\frac{1}{2}\)
(B) \(\frac{3}{4}\)
(C) 1
(D) \(\frac{3}{2}\)
(E) 2
Pembahasan :
Sketsa terlebih dahulu daerah penyelesaian dari sistem pertidaksamaan diatas!
Jawaban : D
12. SBMPTN 2017 Transformasi Geometri
Titik (1, 0) dipetakan dengan translasi \(\begin{pmatrix}
a\\ 2
\end{pmatrix}\) dan kemudian dicerminkan terhadap garis \(\mathrm{x = 3}\) ke titik (6, 2). Peta titik (2, 1) di bawah transformasi yang sama adalah ...
(A) (5, 3)
(B) (6, 2)
(C) (6, 3)
(D) (7, 2)
(E) (7, 3)
Pembahasan :
Peta titik (x, y) oleh translasi (a, b) adalah \(\begin{pmatrix}
\mathrm{x+a}\\ \mathrm{y+b}
\end{pmatrix}\)
Peta titik (x, y) oleh pencerminan terhadap garis x = k adalah \(\begin{pmatrix}
\mathrm{2k-x}\\ \mathrm{y}
\end{pmatrix}\)
Berdasarkan sifat diatas maka :
Peta titik (1, 0) oleh translasi (a, 2) adalah \(\begin{pmatrix}
\mathrm{1+a}\\ \mathrm{0+2}
\end{pmatrix}=\begin{pmatrix}
\mathrm{1+a}\\ 2
\end{pmatrix}\).
Peta titik (1+a, 2) oleh pencerminan terhadap garis \(\mathrm{x = 3}\) adalah \(\begin{pmatrix}
\mathrm{2(3)-(1+a)}\\ \mathrm{2}
\end{pmatrix}=\begin{pmatrix}
\mathrm{5-a}\\ 2
\end{pmatrix}.\)
Diketahui hasil petanya adalah (6, 2), sehingga diperoleh persamaan \(\begin{pmatrix}
\mathrm{5-a}\\ 2
\end{pmatrix}=\begin{pmatrix}
6\\ 2
\end{pmatrix}\).
Dari persamaan diatas diperoleh
5 - a = 6
a = -1
Selanjutnya, akan ditentukan peta titik (2, 1) oleh transformasi yang sama, yaitu translasi (-1, 2) dan dilanjutkan pencerminan terhadap garis x = 3.
Peta titik (2, 1) oleh translasi (-1, 2) adalah \(\begin{pmatrix}
2+(-1)\\ 1+2
\end{pmatrix}=\begin{pmatrix}
1\\ 3
\end{pmatrix}\).
Peta titik (1, 3) oleh pencerminan terhadap garis x = 3 adalah \(\begin{pmatrix}
2(3)-1\\ 3
\end{pmatrix}=\begin{pmatrix}
5\\ 3
\end{pmatrix}\).
Jawaban : A
13. SBMPTN 2017 Integral Tak Tentu
\(\int \mathrm{\frac{3(1\,-\,x)}{1\,+\,\sqrt{x}}\;dx=...}\)
(A) 3x - 2x√x + C
(B) 2x - 3x√x + C
(C) 3x√x - 2x + C
(D) 2x√x - 3x + C
(E) 3x + 2x√x + C
Pembahasan :
\(\begin{align}
\mathrm{\int \frac{3(1-x)}{1+\sqrt{x}}\;dx} & = \mathrm{3\int \frac{\left (1+\sqrt{x} \right )\left ( 1-\sqrt{x} \right )}{1+\sqrt{x}}\;dx} \\
& = \mathrm{3\int (1-\sqrt{x})\;dx} \\
& = \mathrm{3\left ( x-\frac{2}{3}x^{\frac{3}{2}} \right )+C} \\
& = \mathrm{3x-2x^{\frac{3}{2}}+C} \\
& = \mathrm{3x-2x\sqrt{x}+C}
\end{align}\)
Jawaban : A
14. SBMPTN 2017 Limit Tak Tentu
Jika kurva f(x) = ax2 + bx + c memotong sumby-y di titik (0, 1) dan \(\mathrm{_{x \to 1 }^{lim}\;\frac{f(x)}{x\,-\,1}=-4}\), maka \(\frac{b\,+\,c}{a}=...\)
(A) -1
(B) -\(\frac{1}{2}\)
(C) 0
(D) 1
(E) \(\frac{3}{2}\)
Pembahasan :
Karena kurva f(x) = ax2 + bx + c memotong sumbu-y di titik (0, 1), maka c = 1.
Limit diatas merupakan bentuk limit tak tentu 0/0, dapat kita identifikasi dari penyebutnya yang bernilai nol ketika x = 1, sedangkan limitnya ada, yaitu -4. Jadi, haruslah f(1) = 0.
f(1) = a(1)2 + b(1) + 1 = 0 atau
a + b = -1 ............................................(1)
Dengan menggunakan aturan L'Hospital pada \(\mathrm{_{x \to 1 }^{lim}\;\frac{\mathit{a}x^{2}+\mathit{b}x+\mathit{c}}{x\,-\,1}=-4}\) diperoleh
\(\mathrm{_{x \to 1 }^{lim}\;\frac{2\mathit{a}x+\mathit{b}}{1}=-4}\)
2a(1) + b = -4
2a
Eliminasi (1) dan (2) diperoleh a = -3 dan b = 2.
Jadi, \(\frac{b\,+\,c}{a}\) = \(\frac{2\,+\,1}{-3}\) = -1
Jawaban : A
15. SBMPTN 2017 Kaedah Pencacahan
Banyak susunan berfoto berjajar untuk 3 pasang pemain bulutangkis ganda dengan tidak setiap pemain dan pasangannya berdekatan adalah...
(A) 720
(B) 705
(C) 672
(D) 48
(E) 15
Pembahasan :
Banyak susunan dengan tidak setiap pemain dan pasangannya berdekatan dapat dihitung dari selisih banyaknya susunan bebas dengan banyaknya susunan setiap pemain dan pasangannya berdekatan.
Banyak susunan pemain dengan susunan bebas adalah 6! = 720.
Banyak susunan pemain dengan setiap pemain dan pasangannya berdekatan adalah
(A1 A2) (B1 B2) (C1 C2) = 3! . 2! . 2! . 2! = 48
Jadi, banyak susunan dengan tidak setiap pemain dan pasangannya berdekatan adalah
720 - 48 = 672
Jawaban : C



EmoticonEmoticon